Casadirectx 12x

1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =

Por um escritor misterioso
Last updated 17 fevereiro 2025
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
An equation of a parabola is given. (a) Find the focus, dire
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
SOLVED: Use the given equation to identify the direction the parabola is opening, and the vertex, focus, and directrix for the parabola. Then, graph the parabola. Include the focus, vertex, directrix, and
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find the major axis, minor axis, foci and graph an ellipse
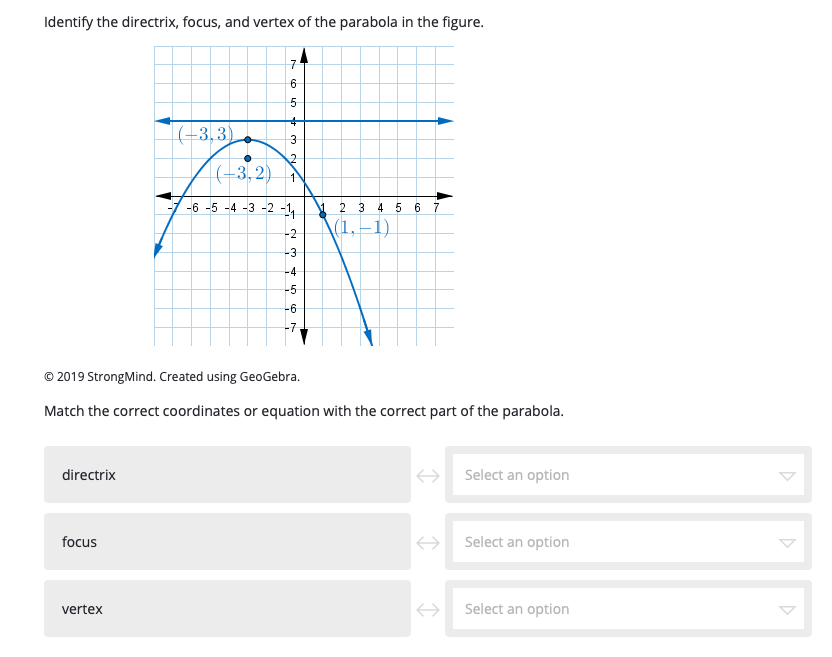
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Answered: Identify the directrix, focus, and…
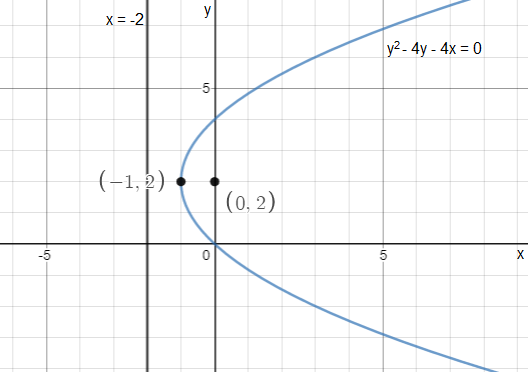
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find the vertex, focus, and directrix of the parabola, and s
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
How to tell if a hyperbola opens up or down - Quora
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved 1. Use the definition of the parabola to write an
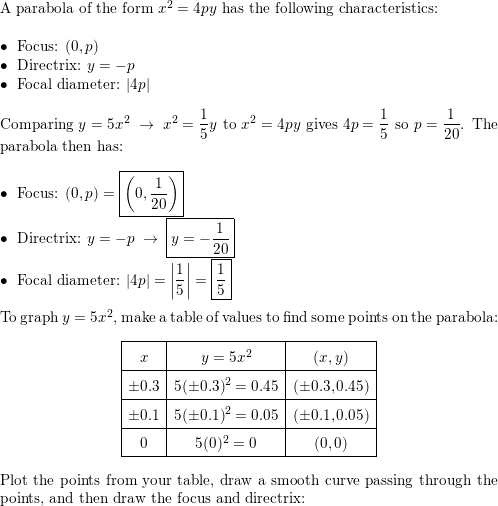
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find the focus, directrix, and focal diameter of the parabol
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
4 Parabolas WS #2-1.pdf - Name Parabolas Worksheet #2 Write the equation of each parabola described below. 1. Vertex -2 3 and focus 4 3 3. Focus
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Write a polar equation of a conic with the focus at the orig
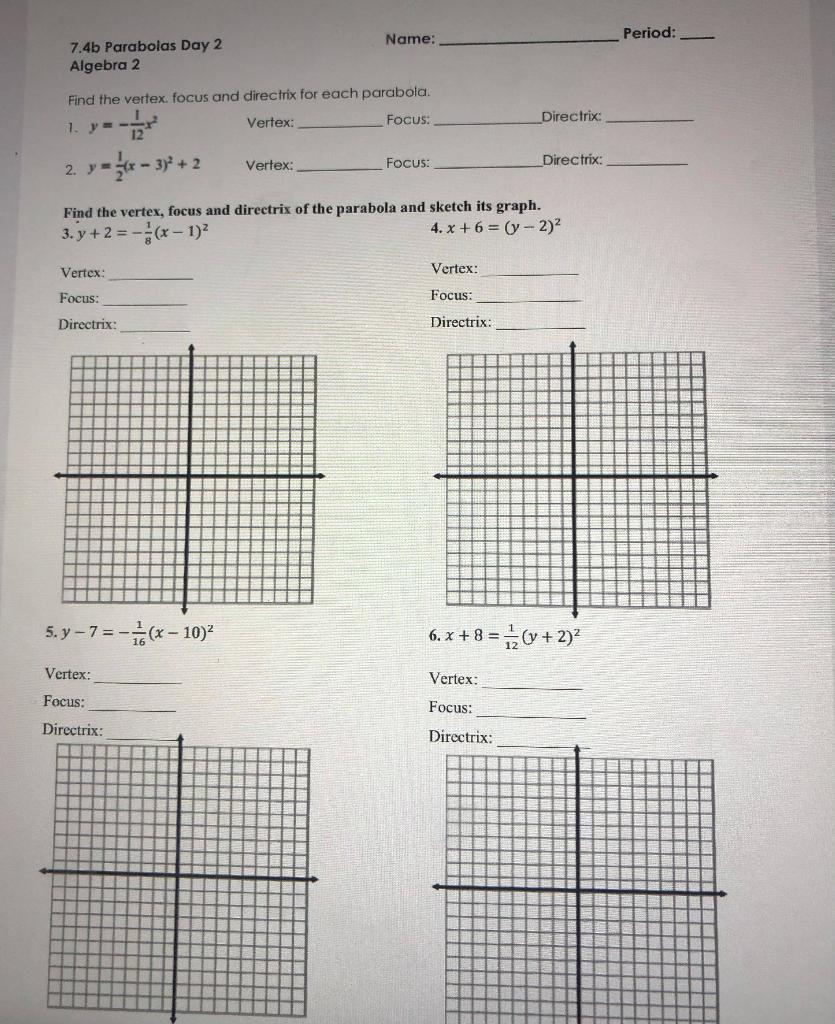
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved Name: Period: 7.4b Parabolas Day 2 Algebra 2 Find the
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
How can I calculate properly the graph of a quadratic function? - Mathematics Stack Exchange
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find a polar equation of the conic with its focus at the pole. Parabola; (8, 0)
Recomendado para você
você pode gostar

© 2014-2025 radioexcelente.pe. All rights reserved.